蛋白代谢多组学研究思路和方法随笔

2024-04-07

字数统计: 4.9k字 | 阅读时长≈ 17分

上一期介绍了关于组学数据的一些基本分析方法，当我们那搭配样本的组学数据之后，能够基于基因的表达量和样本的分组信息进一步筛选biomarker（idea1、idea2），同时进一步结合样本的临床、生理病理、生化等作为一种性状数据（idea3），整合基因的表达，筛选出受到基因表达影响的某种关键性状相关基因集，常见的方法如下。

1.idea1 差异分析+功能分析

对基因的表达量进行不同组间的差异分析或者共表达分析，然后结合数据库的注释结果，分析基因功能或者互作关系，最终目的是找到有生物学意义的差异表达基因。

1.1 差异分析

当获得了可以进行分析的数据之后，我们可以继续基于表达丰度，在大量的样本研究中寻找不同组件的差异表达基因或者蛋白。

其中，转录组的差异分析使用DESeq2、EdgeR方法，不过目前研究发现，大样本量的研究中，这两种方法也存在假阳性的情况，所以个人建议使用Wilcoxon rank sum test的非参数检验进行分析。蛋白组的差异分析经常用方差分析、T检验以及基于DEqMS的R包进行差异分析。关于DEqMS的R包使用，这里有一个简单的例子：

DEqMS（Differential Expression analysis for Quantitative Mass Spectrometry）是一个用于基于质谱的定量蛋白质组学数据差异表达分析的R包。它可以帮助研究人员识别在不同条件或组之间表达水平有显著变化的蛋白质。

安装和加载DEqMS包
如果你尚未安装DEqMS包，请先安装它。在R中，你可以使用以下命令安装：

1
2
3

if (!requireNamespace("BiocManager", quietly = TRUE))
    install.packages("BiocManager")
BiocManager::install("DEqMS")

然后加载DEqMS包：

1	library(DEqMS)

准备数据
DEqMS需要两个主要的数据输入：蛋白质定量值和对应的蛋白质注释信息。定量值通常来自于质谱仪器的输出，而注释信息则包含了蛋白质的 accession number、基因符号等。
假设您已经有了一个包含蛋白质定量值的dataframe，名为protein_expression，以及一个包含蛋白质注释信息的dataframe，名为protein_annotations。

数据预处理
在进行差异表达分析之前，通常需要对数据进行预处理，例如去除缺失值、标准化等。

# 假设我们的定量数据在名为Intensity的列中
# 我们将使用DEqMS中的normalize()函数进行标准化
normalized_data <- DEqMS::normalize(protein_expression$Intensity)

# 将标准化后的数据合并回原来的dataframe
protein_expression$Normalized_Intensity <- normalized_data

设置比较组
在进行差异表达分析之前，您需要定义要比较的组别。这通常通过创建一个设计矩阵来实现。

# 假设我们有两个组别：对照组和治疗组
# 我们创建一个名为Group的列，其中对照组为1，治疗组为2
protein_expression$Group <- ifelse(protein_expression$Condition == "Control", 1, 2)

# 创建设计矩阵
design <- model.matrix(~0 + protein_expression$Group)
colnames(design) <- c("Control", "Treatment")

进行差异表达分析
使用DEqMS包中的runDEqMS()函数进行差异表达分析。

# 假设我们关注的是治疗组与对照组的差异
# 设置对比矩阵，这里我们关注治疗组相对于对照组的差异
contrast.matrix <- makeContrasts(Treatment - Control, levels = design)

# 运行差异表达分析
DE.results <- DEqMS::runDEqMS(protein_expression, design, contrast.matrix)

结果解读
DE.results中包含了差异表达分析的结果，您可以查看哪些蛋白质在不同的组别中显著差异表达。
1
2
# 查看显著差异表达的蛋白质
significant.proteins <- DE.results[DE.results$padj < 0.05, ]
可视化
DEqMS包也提供了一些可视化工具，帮助您更直观地查看分析结果。
1
2
3
4
5
# 绘制火山图
volcanoPlot(DE.results, logFC.cutoff = 0.58, p.cutoff = 0.05)

# 绘制MA图
MAplot(DE.results, cutoff = 0.05)
以上步骤仅为一个简单的示例，实际使用时，你可能需要根据具体的数据格式和分析需求进行调整。DEqMS包的官方文档提供了更详细的参数设置和函数说明。

此外，线性回归分析用于评估基因丰度与其他因素之间的关系，用于特征基因的筛选。线性，也就是可以用一个量化的解释变量来预测一个量化的响应变量；回归则是通过历史数据进行预测。我们如果想要更好的了解基因集之间的一些潜在联系，可以考虑使用LASSO回归方法（least absolute shrinkage and selection operator）。

LASSO(Least Absolute Shrinkage and Selection Operator)是最常用的方法之一，以缩小变量集为核心思想的压缩方法，使某些不重要变量的回归系数变为0，从而选择对因变量影响较大的自变量并计算出相应的回归系数，进行下游分析，交叉验证用于确证结果中的取值是否最佳。

1.2功能分析

功能分析旨在系统性地揭示显著表达变化基因的功能内涵及其在复杂生物过程中的作用机制，需要明白下面这些事情

1）. 目标明确：基因功能与通路解析

基因功能探索：

分子功能：揭示显著差异基因在生物化学反应、分子互动、结构构成等方面的特定功能，如酶活性、受体结合、信号转导等。
生物过程：定位差异基因参与的生理或病理过程，如细胞周期调控、免疫应答、代谢途径、神经传导等。
细胞组分：阐明差异基因在细胞结构、亚细胞器、细胞间通讯等层面的作用，如细胞膜、线粒体、细胞核、分泌囊泡等。

通路解析：

关键通路识别：聚焦与研究目的密切相关的显著变化通路，如癌症相关的PI3K/AKT/mTOR通路、炎症反应的NF-κB通路、细胞凋亡的Caspase通路等。
通路动态：分析通路内基因的整体表达趋势（上调、下调）和相对丰度变化，揭示通路在特定条件下的激活、抑制或重塑状态。

2）多维度数据整合与深度解析

基因注释：

详细注释信息：从GO、KEGG、Reactome、DO等数据库获取差异基因的详细注释信息，包括但不限于：GO术语、通路名称、疾病关联、药物靶点等。
层次化注释：按照分子功能、生物过程、细胞组分三个层次进行注释，构建差异基因的多层次生物学属性图谱。

富集分析：

统计学检验：
- 超几何检验：针对每个预定义的生物学类别（如GO术语、KEGG通路），计算差异基因的富集概率，评估其在该类别中的过表达或欠表达是否显著。
- 多重校正：应用FDR校正或其他方法控制假阳性率，确保富集结果的统计学可靠性。
全局表达谱分析：
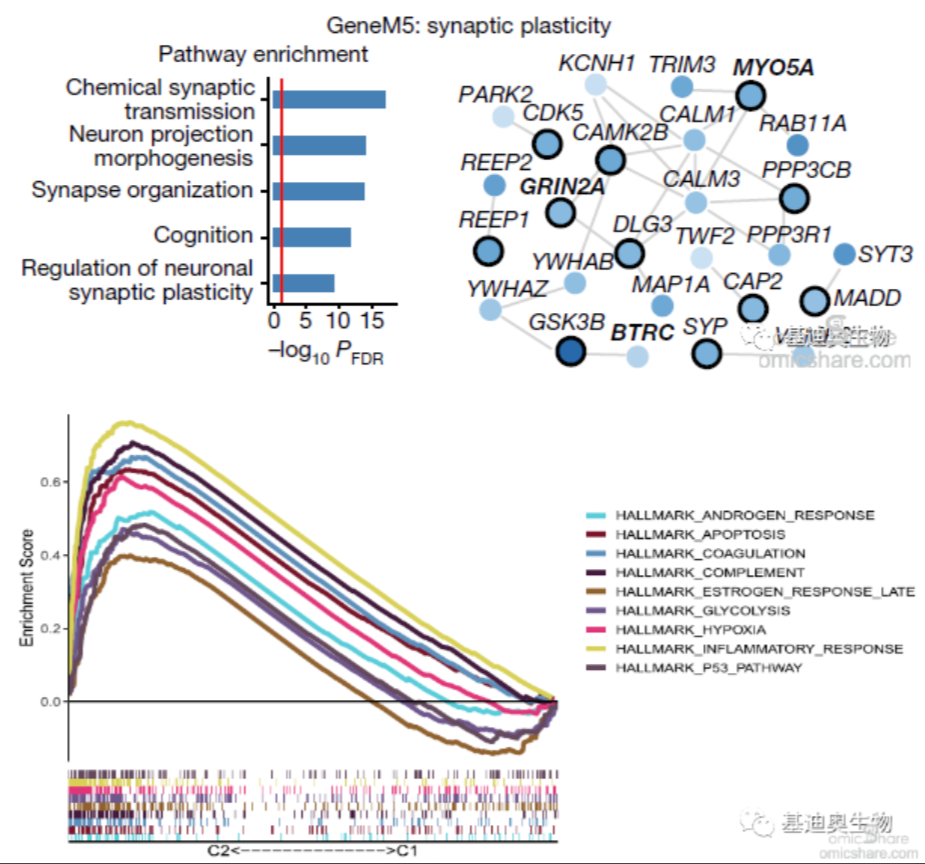
- GSEA：根据整个基因集在表达谱中的排名，评估预定义基因集（如MSigDB中的C2、C5集合）与样本分组间的关联强度，识别在整体丰度变化中具有显著意义的基因集。
- 权重得分：计算基因集的NES（Normalized Enrichment Score）或ES（Enrichment Score），反映基因集的富集程度和方向。

调控网络构建：

蛋白质互作网络：利用STRING数据库，基于实验验证、同源性推断、文本挖掘等多种证据来源，构建差异蛋白间的直接或间接互作关系网络。
网络特性分析：
- 核心蛋白识别：计算节点的度、介数、聚类系数等网络指标，识别在网络中占据中心位置、可能发挥关键调控作用的核心蛋白。
- 模块划分：运用社区检测算法，将网络划分为多个功能相关的子模块，揭示潜在的调控子系统。

多层次关联：

转录因子靶基因预测：利用ENCODE、ChIP-seq等数据资源，预测差异基因作为特定转录因子靶点的可能性，揭示转录调控网络的变化。
miRNA调控分析：结合miRNA表达数据和靶基因预测软件（如TargetScan、miRanda），分析差异基因是否受到差异表达miRNA的调控。
表观遗传学关联：考察差异基因的DNA甲基化、组蛋白修饰、染色质开放性等表观遗传标记的变化，揭示表观遗传调控与基因表达变化的关联。

3）生物学意义诠释与应用前景

结果解读：

生物学机制推测：结合富集分析结果和现有文献，推测显著通路或功能在研究背景下的具体作用机制，如通路激活如何驱动肿瘤进展、特定功能如何影响细胞分化等。
因果关系推理：根据差异基因在通路中的位置、功能和表达变化，推断其在特定生物学过程中的因果作用，如上游激酶的激活如何导致下游效应基因的表达上调。

可视化展示：

富集结果可视化：绘制条形图、火山图、富集热图等，直观展示显著富集的GO术语、KEGG通路及其统计显著性。
网络图可视化：利用Cytoscape等工具绘制蛋白质互作网络、转录因子调控网络等，通过节点颜色、大小、形状等视觉元素展示基因属性和网络特性。

实验验证与应用导向：

候选基因/通路验证：设计qPCR、Western blot、CRISPR/Cas9敲除/过表达、小分子药物处理等实验，验证候选基因的功能效应、基因-通路关联、基因-表型关联等。
临床应用潜力评估：
- 诊断标志物：分析差异基因或通路在患者队列中的表达模式，评估其作为疾病分类、预后预测或疗效监控标志物的潜力。
- 治疗靶点：研究针对核心蛋白或关键通路的小分子抑制剂、抗体药物、基因疗法等，评估其作为治疗策略的有效性和安全性。

因此，功能分析是一项深入而细致的研究工作，它通过多维度数据整合、深度的生物信息学解析、严谨的生物学意义诠释和实验验证，全面揭示基因表达数据背后的生物学故事，解释相关的疾病致病机制和蛋白作用机制。

1.3 相关性分析

相关性分析是指对两个或以上的具有潜在相关性的变量进行的关联分析，根据变量的变化模式/规律，利用得到的相关系数来评估两个或以上的变量元素的相关密切程度。相关系数一般介于-1~1之间，绝对值越靠近1，相关性越强，其中-1为完全负相关，1为完全正相关，0为不相关。

1）Pearson相关系数（也称为皮尔逊积矩相关系数）基于协方差的概念，它是衡量两个随机变量间线性相关程度的统计量。其计算公式为：

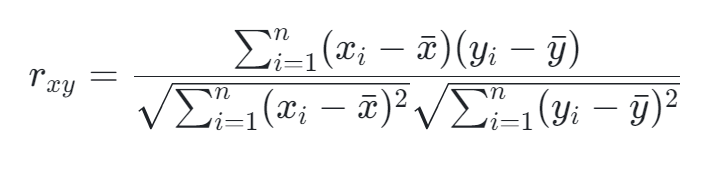
计算过程中，首先通过标准化处理消除量纲影响和数据尺度差异，然后计算变量间协方差与各自标准差的乘积，最终得到一个无量纲的系数。只有当数据满足正态分布且变量间存在线性关系时，Pearson相关系数才最具解释力。

2）Spearman秩相关系数是一种非参数统计方法，它基于秩次统计而非原始数值进行计算。其基本思想是将每个变量的所有观测值按照大小排序，赋予相应的秩次，然后计算这两个秩序列间的相关性。计算公式为：

由于其计算过程不涉及原始数值，而是关注变量间的排序关系，因此对数据分布类型和异常值不敏感，适用于非正态分布数据和等级数据的关联分析。它基于每个变量的排名值而非原始数据，使用单调函数来描述两个变量之间的关系程度，获取两个变量元素之间的变化趋势。那么当数据符合正态分布时，分析效率上Spearman与Pearson是等价的。Spearman相关系数同样取值于-1到1之间，性质与Pearson相关系数类似。

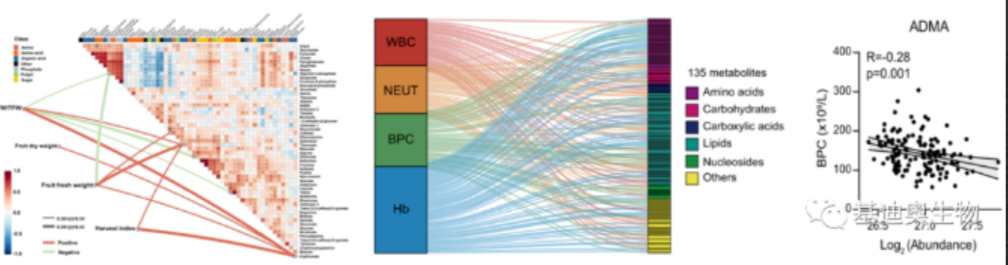
常用可视化包括：热图、桑基图、线性散点图等。

应用场景与实例

Pearson相关应用实例：在金融投资领域，研究者可能运用Pearson相关分析股票价格变动与宏观经济指标（如GDP增长率、失业率等）的关系。若发现两者间存在显著的正相关，投资者可能会据此调整投资策略，预期在经济向好时股票市场表现也将提升。

Spearman相关应用实例：在教育心理学研究中，为探究学生的学习动机与学习成绩之间的关联，但收集到的数据可能存在极端值或非正态分布，此时选择Spearman相关更为合适。即使某些学生的动机得分或成绩偏离常态，只要其相对排序保持一致，Spearman相关仍能有效捕捉动机与成绩间的单调递增或递减关系。

可视化展示

热图：在多元相关性分析中，热图以矩阵形式呈现各变量间的相关系数，颜色深浅代表相关强度。例如，研究者可通过热图快速识别一组健康指标（如血压、血糖、体重等）之间的强弱关联，深红色区块表示高度正相关，深蓝色区块表示高度负相关，白色或浅色表示无明显关联。

桑基图：尽管桑基图主要用于能量流动、资源分配等流程分析，但在特定条件下也可用于展示变量间复杂的相关结构。例如，通过构建桑基图可以直观展示不同行业板块股票收益率之间的资金流动与相关性，箭头宽度代表资金流量，颜色编码表示相关性强弱，从而揭示股市中各板块间的联动效应。

线性散点图：这是最直观的二维相关性可视化工具。每个数据点代表一对变量观测值，点的分布模式揭示了变量间是否存在线性趋势。例如，绘制年龄与收入的散点图，若点大致沿一条直线分布，且斜率为正，说明年龄与收入呈正相关；反之，若点分布呈反向倾斜，说明两者负相关。通过拟合最佳线性回归线（通常为最小二乘法），可进一步量化这种线性关系。

平行坐标图 (Parallel Coordinates Plot):
这种图形适合展示多维数据集中变量间的相关性。每个数据点在多个垂直平行轴上表示其在各个维度上的值，通过连接同一数据点在各轴上的投影形成一条折线。观察折线的分布和交叉情况，可以直观识别变量间的关联模式。例如，在研究汽车性能时，可以使用平行坐标图展示车辆重量、马力、燃油效率、价格等多个属性之间的相互关系，寻找是否存在某些属性组合（如高马力与高价格）经常同时出现。

网络图 (Network Graph):
网络图用于展示变量之间的复杂关联结构，特别是当变量间的关系并非简单的一对一对应时。节点代表变量，边的权重或颜色表示变量间的相关性强度。在网络图中，簇状结构或中心节点的存在往往暗示着变量间的强相关或核心关联。例如，在社交媒体数据分析中，可以构建用户行为网络图，节点代表用户，边的权重依据用户间的互动频率（如共同发帖、点赞、评论等）确定，从而揭示用户群体间的社交网络结构及其相关性。

雷达图 (Radar Chart):
雷达图特别适用于展示个体在多个维度上的表现及其相对优势或劣势。虽然雷达图主要用来比较不同实体在多变量上的整体概况，但它也能间接反映变量间的相关性。如果一个实体在某几个变量上的得分高度相关（即同时高或同时低），那么这些变量在雷达图上的“尖角”会靠近，形成明显的关联特征。例如，在评估员工绩效时，雷达图可以展示员工在技能、沟通能力、项目完成度、团队协作等多方面的得分，通过观察图形形态，可以判断各项能力间是否存在协同效应或互补关系。

气泡图 (Bubble Chart):
气泡图是散点图的一种变体，除了用点的位置表示两个变量的关系外，还通过点的大小表示第三个变量的值。这种图形有助于同时展示三元关系中的相关性和变量强度。例如，在分析公司市值、利润和员工数量之间的关系时，可以用横纵坐标分别表示市值和利润，气泡大小代表员工数量。观察气泡的分布和大小变化，可以发现市值与利润之间的线性关系，以及员工数量对此关系的影响。

马赛克图 (Mosaic Plot) 或条形图矩阵:
这两种图形常用于展示分类变量间的联合分布和条件概率，特别适用于离散型数据。它们通过矩形面积的相对大小来直观表示各类别组合的频数或比例，从而揭示类别间的关联性。例如，在市场调研中，可以创建马赛克图或条形图矩阵展示消费者性别、年龄层次与购买偏好（如电子产品、服装、食品等类别）的联合分布，直观看出哪些性别和年龄段的消费者更倾向于购买特定类型的商品。

动态可视化:
随着数据科学和信息技术的发展，动态可视化越来越受到青睐。通过动画、滑动条或交互式界面，用户可以随时间推移观察相关性变化，或者在不同参数设置下探索相关性模式。例如，可以制作一个动态散点图，随着时间滑块移动，显示股票价格与市场情绪指标（如新闻情绪分析得分）之间的实时相关性变化，帮助投资者理解市场情绪如何影响股价波动。

本文作者： Anderson
本文链接： http://nikolahuang.github.io/2024/04/07/蛋白代谢多组学研究思路和方法随笔/
版权声明： 转载请注明出处，谢谢。